DSA: Intervals

Fundamentals of Intervals

What to Look Out For

Corner Cases

Common Techniques

Practice Problems

Learning Resources

---

Fundamentals of Intervals

Interval questions are a subset of array questions where you are given an array of two-element arrays (an interval) and the two values represent a start and an end value. Interval questions are considered part of the array family but they involve some common techniques hence they are extracted out to this special section of their own.

An example interval array: [[1, 2], [4, 7]].

Given two intervals (‘A’ and ‘B’), there will be six different ways the two intervals can relate to each other:

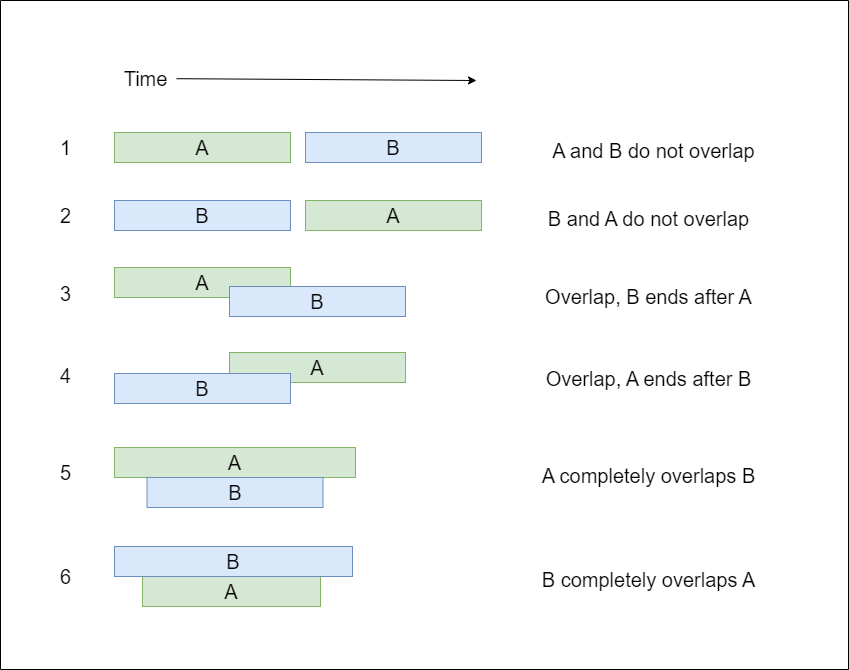
What to Look Out For

• Clarify with the interviewer whether [1, 2] and [2, 3] are considered overlapping intervals as it affects how you will write your equality checks.

• Clarify whether an interval of [a, b] will strictly follow a < b (a is smaller than b)

Corner Cases​

• No intervals

• Single interval

• Two intervals

• Non-overlapping intervals

• An interval totally consumed within another interval

• Duplicate intervals (exactly the same start and end)

• Intervals which start right where another interval ends - [[1, 2], [2, 3]]

---

Common Techniques

Sort Intervals

Typically, you want to sort the intervals by their starting point.

#sort method
intervals.sort()

#sorted method with lambda
sorted_intervals = sorted(intervals, key=lambda x : x[0])

Check if Intervals Overlap:

def is_overlap(a, b):
  return not(a[1] < b[0] or b[1] < a[0])

Merge Two Intervals:

def merge_overlapping_intervals(a, b):
  return [min(a[0], b[0]), max(a[1], b[1])]	

Readable Code:

It's a lot easier to read code regarding intervals if you create start and end variables rather than using 0 and 1.

interval = [2, 5]

start, end = 0, 1

interval[start] # 2
interval[end] # 5

---

Practice Problems

Merge Intervals

def mergeIntervals(intervals):
    intervals.sort() # Sort the intervals
    
    start, end = 0, 1
    result = []

    def overlap(a, b): #Define a function to find overlaps
        return not(a[1] < b[0] or b[1] < a[0])
    
    for interval in intervals:
        # If no result or no overlaps, append interval
        if len(result) == 0 or not overlap(result[-1], interval):
            result.append(interval)
        else:
            result[-1][end] = max(result[-1][end], interval[end])
    
    return result

Insert Interval

Meeting Rooms

Meeting Rooms II

Intersection of Intervals

---

Learning Resources