DSA: Disjoint Union Set

Union Find Fundamentals

Union Find Template

Practice Problems

Learning Resources

---

Union Find Fundamentals

Imagine we have sets of nodes or elements and are asked to check if they belong to a specific set. To solve this kind of question, we can use a union find algorithm on a disjoin union set to visualize our data as a series of trees where certain elements belong to one set only. In this algorithm, we essentially assign one node as the leader/parent of a group and have other nodes point to that parent node's value and save it in a set. That way, if all nodes have one shared parent, we know they belong to that group. Take a look at the illustration below to get a better understanding of this.

---

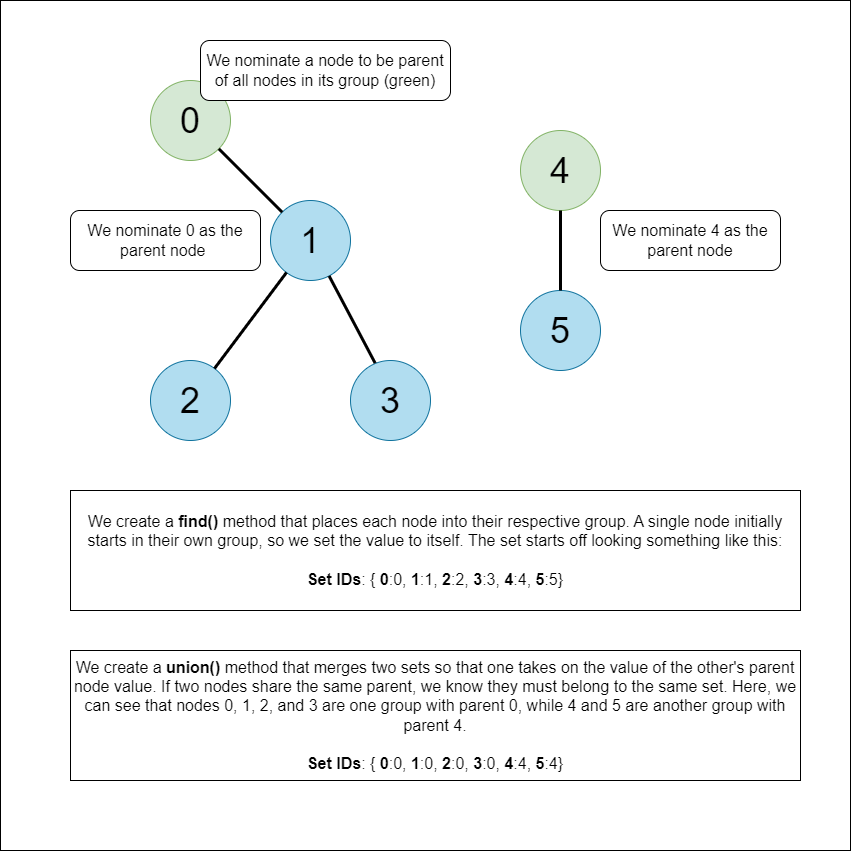
Union Find Template

Basic Implementation

class UnionFind:
    # initialize the data structure that maps the node to its set ID
    def __init__(self):
        self.id = {}

    # find the Set ID of Node x
    def find(self, x):
        # get the value associated with key x, if not in map return x
        y = self.id.get(x, x)
        # check if the current node is a Set ID node
        if y != x:
            # set the value to Set ID node of node y
            y = self.find(y)
        return y

   # union two different sets setting one Set's parent to the other parent
    def union(self, x, y):
        self.id[self.find(x)] = self.find(y)

Optimized Implementation

class UnionFind:
    def __init__(self):
        self.id = {}

    def find(self, x):
        y = self.id.get(x, x)
        if y != x:
        # set the value to Set ID node of node y, and change the hash 
          value of node x to Set ID value of node y
            self.id[x] = y = self.find(y)
        return y

    def union(self, x, y):
        self.id[self.find(x)] = self.find(y)

The following code accomplishes a union operation in O(1) and a find operation that has best case O(1), average case O(log(n)) since we have a randomized trees which have average depth O(log(n)) and a worst case of O(n) for a maximum depth tree.

---

Practice Problems

Same Set

Problem:

Complete the class below to support the following two operations:

1. merge(x, y) merges the sets that the x and y belong to,

2. is_same(x, y) determines if x and y belong to the same set. If so return true, otherwise false.

Example:

merge(1, 2)
merge(2, 3)
is_same(1, 3) => true
is_same(2, 4) => false

Solution:

class UnionFind:
    ...

class SameSet:
    def __init__(self) -> None:
        self.dsu = UnionFind()

    def merge(self, x, y):
        self.dsu.union(x, y)

    def is_same(self, x, y):
        return self.dsu.find(x) == self.dsu.find(y) 

Time Complexity: O(nlog(n))

Space Complexity:

Size of Connected Components

Problem:

Similar to the last problem, this time instead of checking whether or not 2 values belong to the same set, we want to know the size of the set that a value belongs to. Therefore, we now support a different set of 2 operations:

1. merge(x, y) merge the sets that x and y belong to,

2. count(x) returns the size of the set that x belongs to.

Example:

merge(1, 2)
merge(2, 3)
count(3) => 3
count(4) => 1

Solution:

class UnionFind:
    ...

class SetCounter:
    def __init__(self) -> None:
        self.dsu = UnionFind()
        self.sizes = {}

    def merge(self, x, y):
        if self.dsu.find(x) != self.dsu.find(y):
            new_size = self.count(x) + self.count(y)
            self.dsu.union(x, y)
            self.sizes[self.dsu.find(x)] = new_size

    def count(self, x):
        return self.sizes.get(self.dsu.find(x), 1)

Time Complexity: O(nlog(n))

Space Complexity:

Umbristan

Problem:

You have recently been promoted as the director of infrastructure of Umbristan. Congratulations! Our Duke Stack Umbristan has recently ordered the destruction of all the roads of Umbristan so that new ones can be rebuilt. Our Duke has assigned you, the director of infrastructure, an important task. After each road in Umbristan is demolished he wants to know how many clusters of cities will still be connected after the road is destroyed. Two cities are considered connected if there exists a series of roads one can take to travel to reach one city from another. A cluster of cities being connected means that for any 2 cities in the cluster there exists a path between the 2 cities. The input will first consist of the number n which is the number of cities numbered from 1 to n. Then there will exist a list of roads that represent the road connecting 2 cities is now broken. Each road in this list is guaranteed to be a valid existing road. The final result will be guaranteed to have no roads(since all roads must be destroyed).

Example:

Input: n = 4, breaks = [[1, 2], [2, 3], [3, 4], [1, 4], [2, 4]]

Output: [1, 1, 2, 3, 4]

Solution:

class UnionFind:
    ...

def umbristan(n, breaks):
# initialize data structures
    dsu = UnionFind()
    breaks.reverse()
    result = []

# loop through the reverse list and merge the edges if they are not of the same list
    for a, b in breaks:
        result.append(n)
# merging 2 connected components means total number of connected components decreases by 1
        if dsu.find(a) != dsu.find(b):
            dsu.union(a, b)
            n -= 1
            
# remember that our answers are in reverse since we started from the end
    result.reverse()
    return result 

Time Complexity: O(nlog(n))

Space Complexity:

Accounts Merge

Problem:

Given a list of accounts where each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account.

Now, we would like to merge these accounts. Two accounts definitely belong to the same person if there is some common email to both accounts. Note that even if two accounts have the same name, they may belong to different people as people could have the same name. A person can have any number of accounts initially, but all of their accounts definitely have the same name.

After merging the accounts, return the accounts in the following format: the first element of each account is the name, and the rest of the elements are emails in sorted order. The accounts themselves can be returned in any order.

Example:

Input:

accounts = [
  ["John", "johnsmith@mail.com", "john_newyork@mail.com"],
  ["John", "johnsmith@mail.com", "john_work@mail.com"],
  ["Mary", "mary@mail.com"],
  ["John", "johnny@mail.com"]
]

Output:

[ 
   ["John", "john_newyork@mail.com", 
    "john_work@mail.com",
    "johnsmith@mail.com"], 
   ["John", "johnny@mail.com"], 
   ["Mary", "mary@mail.com"], 
]

Solution:

class UnionFind:
    ...

def merge_accounts(accounts):
    # Declare variables
    union_find = UnionFind()
    all_user_emails = set()

    # loop through accounts
    for one_account in accounts:
        # get user 
        username = one_account[0]
        email_parent = None

        #loop through emails in one account
        for email in one_account[1:]:
            user_email_pair = (username, email)
            # add pair to set
            all_user_emails.add(user_email_pair)

            if email_parent is None:
                email_parent = user_email_pair
            else:
                union_find.union(email_parent, user_email_pair)
    
    
    account_associations = {}
    for user_email_pair in all_user_emails:
        ancestor = union_find.find(user_email_pair)
        if ancestor not in account_associations:
            account_associations[ancestor] = []
        account_associations[ancestor].append(user_email_pair)
    return_res = []
    
    for user in account_associations:
        one_user = [user[0]]
        for email in sorted(account_associations[user]):
            one_user.append(email[1])
        return_res.append(one_user)

    return sorted(return_res, key = lambda a: (a[0], a[1]))

Time Complexity: O(nlog(n))

Space Complexity:

Leetcode: Accounts Merge - LeetCode

Number of Connected Components

Problem:

You have a graph of n nodes. You are given an integer n and an array edges where

edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.

Return the number of connected components in the graph.

Example:

Input: n = 5, edges = [[0,1],[1,2],[3,4]] Output: 2

Solution:

class UnionFind:
    ...

def number_of_connected_components(n, edges):
# dsu initialization, this should look familiar
    result = []
    connected_components = n
    dsu = UnionFind()
    for a, b in edges:
# check if they are part of the same set if not merge and decrease connected components by 1
        if dsu.find(a) != dsu.find(b):
            dsu.union(a, b)
            connected_components -= 1
        result.append(connected_components)
    return result

Time Complexity: O(nlog(n))

Space Complexity:

Leetcode: Number of Connected Components in an Undirected Graph - LeetCode

Number of Islands

Number of Islands II

Graph Valid Tree

Redundant Connection

Redundant Connection II

Friend Circles

Sentence Similarity

---

Learning Resources

1. Union find - Algorithmist

2. Leetcode-Union-Find Data Sturcture | by Yunrui Li | Medium