DSA: Topological Sort

Fundamentals of Topological Sort

Topological Sort Template

Practice Problems

Learning Resources

---

Fundamentals of Topological Sort

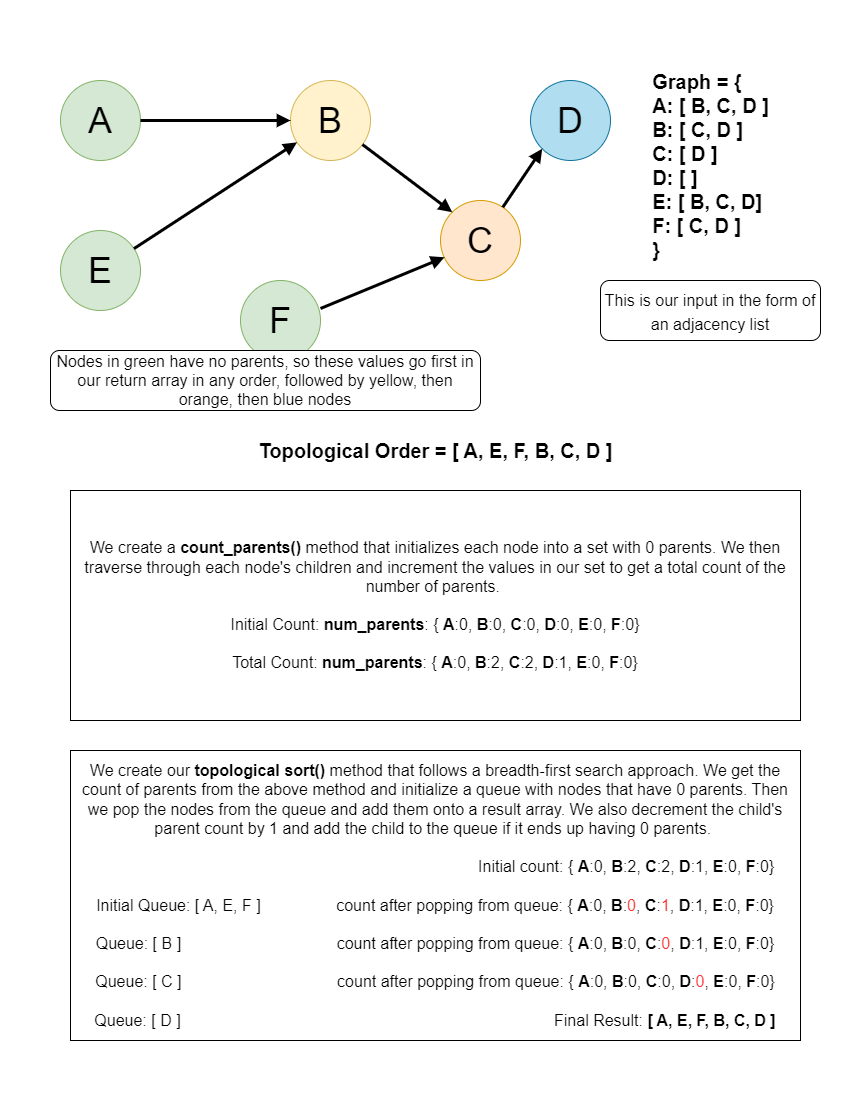
Let's summarize the steps here:

1. Initialize a hashmap of node to parent count.

2. Go through the nodes, count how many parents each node has (a parent node means another node pointing to the current).

3. Push the nodes with 0 parents into the queue.

4. Pop each node from the queue, subtract 1 from the parent count of each node it points to.

5. If a node's parent count drops to 0, then push it into the queue.

6. repeat until the queue is empty. If the queue is not empty, then there must be a cycle.

Note that graphs with cycles don't have topological ordering.

---

Topological Sort Template

Problem:

topological_order({
  "a": ["f"],
  "b": ["d"],
  "c": ["a", "f"],
  "d": ["e"],
  "e": [],
  "f": ["b", "e"],
}) # -> ['c', 'a', 'f', 'b', 'd', 'e']

Basic Implementation:

from collections import deque

def count_parents(graph):
    # Initialize nodes in graph with 0 parents
    num_parents = { node: 0 for node in graph }
    
    # For each child, increment parent count of the child
    for parent in graph:
        for node in graph[parent]:
            num_parents[node] += 1
            
    return num_parents

def topo_sort(graph):
    result = []
    queue = deque()
    counts = count_parents(graph)

    for node in counts:
        # Add nodes with 0 parents to the queue
        if counts[node] == 0:
            queue.append(node)
            
    while len(queue):
        node = queue.popleft()
        result.append(node)
        for child in graph[node]:
            # decrement child parent count when removing parent node
            counts[child] -= 1
            
            # if number of parents of child is 0, add to queue
            if counts[child] == 0:
                queue.append(child)

    return result if len(graph) == len(result) else None

Time Complexity: O(V+E). The above algorithm is simply BFS with an extra stack. So time complexity is the same as DFS

Auxiliary space: O(V), The extra space is needed for the 2 stacks used

---

Practice Problems

Task Scheduling 1

Task Scheduling 2

Reconstructing Sequence

Alien Dictionary

Course Schedule

---

Learning Resources